Innhold
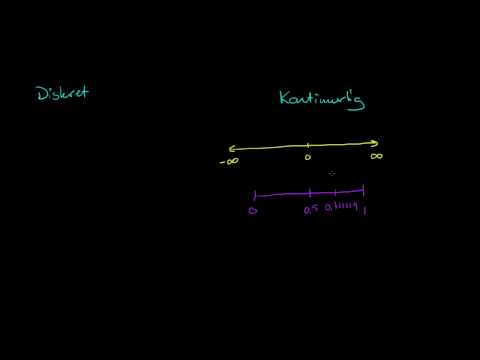
Diskret matematikk er studiet av matematikk begrenset til settet av heltall. Mens applikasjoner av grener av kontinuerlig matematikk, som kalkulator og algebra, er kjent for mange mennesker, kan applikasjonene av diskret matematikk være uklar i begynnelsen. Det danner imidlertid grunnlaget for mange virkelige vitenskapelige områder, særlig datavitenskap. De grunnleggende teknikkene som læres i et diskret matematikk kurs, kan brukes på flere områder.

kryptering
Krypteringsgrenen, som er studien av hvordan man oppretter sikkerhetsstrukturer og passord for datamaskiner og andre elektroniske systemer, er helt basert på diskret matematikk. Dette skyldes blant annet at datamaskiner sender informasjon i diskrete eller små og separate biter. Nummerteori, en viktig del av diskret matematikk, tillater kryptografer å lage og bryte numeriske passord. På grunn av hvor mye penger og konfidensiell informasjon som er involvert, må kryptografer først ha en sterk kunnskapsbase i talteori for å vise at de kan gi sikre passord og utvikle krypteringsmetoder.
Relasjonsdatabase
Relasjonsdatabaser deltar i nesten alle organisasjoner som trenger å holde oversikt over ansatte, kunder eller ressurser. En relasjonsdatabase forbinder egenskapene til et bestemt stykke informasjon. For eksempel, i en database som inneholder kundeinformasjon, kan relasjonsaspektet i denne databasen tillate datasystemet å koble kundens navn, adresse, telefonnummer og annen relevant informasjon. Dette er alt gjort fra begrepet sett med diskret matematikk. Sett gjør at informasjon kan grupperes og plasseres i rekkefølge. Siden hvert stykke informasjon og hver funksjon som tilhører den delen er diskret, organiserer den informasjonen i en database krever diskrete matematiske metoder.
logistikk
Logistikk er studiet av organisering av strømmen av informasjon, varer og tjenester. Uten diskret matematikk ville logistikk ikke eksistere, fordi det gjør stor bruk av grafer og grafteori, et underområde av diskret matematikk. Grafteori tillater komplekse logistiske problemer å bli forenklet til grafer bestående av noder og linjer. En matematiker kan analysere disse grafer i henhold til grafteoriens metoder for å bestemme de beste rutene for å sende eller løse andre logistiske problemer.
algoritmer
Algoritmer er reglene som en datamaskin driver med. Disse reglene er opprettet i henhold til lovene i diskret matematikk. En dataprogrammerer bruker diskret matematikk til å utvikle effektive algoritmer. Denne utviklingen inkluderer anvendelse av diskret matematikk for å bestemme antall trinn algoritmen trenger å fullføre, noe som innebærer algoritmens hastighet. På grunn av applikasjoner av diskret matematikk i algoritmer, er dagens datamaskiner raskere enn de noen gang var.